Powers of 3/2 Modulo One

Given any positive real number x, let

{x} = x mod 1 = x - floor(x)

denote the fractional part of x. For any positive integer n, clearly

{n + x} = {x}

for all x, and the sequence is periodic if x is rational. What can be said about the latter if x is irrational? A consequence of Weyl's criterion [1,39] is that the sequence is dense in the interval [0,1] for irrational x. Moreover, it is uniformly distributed in [0,1], meaning that the probability of finding an arbitrary element in any subinterval is proportional to the subinterval length. We mention more about such sequences in our essay on continued fractions.

Having discussed addition and multiplication, let us turn to exponentiation. Hardy & Littlewood [34] proved that the sequence 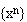is uniformly distributed for almost all real numbers x>1, meaning that the exceptional x form a set of Lebesgue measure zero. Many elements of the exceptional set have been identified (e.g., 2, 3, 4, ... and ), but no specific elements of its complement are known. (See, however, the Postscript.) For the sake of definiteness, fix x=3/2 in the remainder of this discussion.

Pisot [35] and Vijayaraghavan [2] proved that has infinitely many accumulation points, i.e., infinitely many convergent subsequences with distinct limits. The sequence is believed to be uniformly distributed, but no one has even proved that it is dense in [0,1].

Here is a somewhat less ambitious problem: prove that has infinitely many accumulation points in both [0,1/2) and [1/2,1]. In other words, prove that the sequence does not prefer one subinterval over the other. This problem remains unsolved, but Flatto, Lagarias & Pollington [5] recently made some impressive progress. They proved that any subinterval of [0,1] containing all but perhaps finitely many accumulation points of must have length at least 1/3. Therefore the sequence cannot prefer over for any . Likewise, it cannot prefer over . These seemingly intuitive statements required detailed analysis in [5]. To extend the proof to [0,1/2) and [1/2,1] would be a significant but formidable achievement.

Lagarias [6] mentioned the sequence and its loose connections with ergodic-theoretic aspects of the famous 3x+1 problem. The details are too elaborate for us to discuss here. What's fascinating is that the sequence is also fundamental to a seemingly distant area of number theory: Waring's problem on writing integers as sums of nth powers.

Let g(n) denote the smallest integer k for which every positive integer can be expressed as the sum of k nth powers of nonnegative integers. The following table gives values of g(n) for small n plus some historical information [7-11]:

n	g(n)	who proved and when
2	4	J. L. Lagrange (1770)
3	9	A. Wieferich & A. J. Kempner (1912)
4	19	R. Balasubramanian, J.-M. Deshouillers & F. Dress (1986)
5	37	Chen-Jingrun (1964)
6	73	S. Pillai (1940)

For all remaining n>6, Dickson [36,37] and Pillai [38] independently proved that



provided that the condition



is satisfied. So it is sufficient to study this inequality, the last remaining obstacle in the solution of Waring's problem.

Kubina & Wunderlich [13], extending Stemmler [12], verified computationally that the inequality is met for all 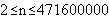. Mahler [14] moreover proved that it fails for at most finitely many n, using Roth's theorem on rational approximations to algebraic numbers. The proof is non-constructive and thus a computer calculation which rules out failure altogether is still not possible.

It appears that the inequality can be strengthened to



for all n>7 and generalized in certain ways [15,16]. Again, no proof is known apart from Mahler's argument. (The best effective results are due to Beukers[17] and Dubitskas[18], with 3/4 replaced by 0.5769.) The fact that so simple an inequality can defy all attempts at analysis is remarkable.

The calculation of g(n) is sometimes called the "ideal" part of Waring's problem. Let G(n) denote the smallest integer k for which all sufficiently large integers can be expressed as the sum of k nth powers of nonnegative integers. We briefly summarize known results for G(n) here.

Postscript

Martin Goldstern has written the following message (which contradicts my assertion that no such x was known):

There is an explicit construction (by M. Levin) of a number x such that 
x^n is uniformly distributed mod 1, and even completely uniformly
distributed, i.e., also the sequence (x^n, x^{n+1}) is uniformly distributed  
in the square, etc.  

Here is an unrelated but interesting fact. Infinitely many integers of the form are composite [22,23] when x=3/2. This is also true when x=4/3. Are infinitely many such integers prime? What can be said for other values of x?

An unrelated conjecture is that, if t is a real number for which 2^t and 3^t are both integers, then t is rational. This would follow from the so-called four exponentials conjecture [25,26]. A weaker result, the six exponentials theorem, is known to be true.

Here is another unrelated but interesting fact. Define an infinite sequence {} by



Odlyzko & Wilf [27] have proved that



for all n, where the constant 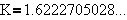(in fact, they proved much more). Their work is connected to the solution of the ancient Josephus problem. Herbert Wilf kindly wrote to me that K is analogous to Mills' constant, in the sense that the formula is useless computationally (unless an exact value for K somehow became available), but its mere existence is remarkable.

A 3-smooth number is a positive integer whose only prime divisors are 2 or 3. A positive integer n possesses a 3-smooth representation if n can be written as a sum of 3-smooth numbers, where no summand divides another. Let r(n) denote the number of 3-smooth representations of n. Some recent papers [29-31] answer the question of the maximal and average orders of r(n).

Let n be an integer larger than 8. Need the base 3 expansion of 2ⁿ possess a digit equal to 2 somewhere? Erdös [32] conjectured that the answer is yes, and Vardi [33] has verified this up to n = 2 * 3²⁰.

More instances of the interplay between the numbers 2 and 3 occur in our essay on triple-free set constants.

References for the new g(4)=19 result include those listed in [24].

Acknowledgements

I thank Victor Miller, Gerry Myerson, Marcus Hum, Martin Goldstern, Timothy Chow and Richard Bumby for pointing out references to me. Another rich source is Reviews in Number Theory, section K25 (compiled from many years of reviews by the American Mathematical Society).

References

1. J. W. S. Cassels, An Introduction to Diophantine Approximation, Cambridge University Press, 1965; MR 50 #2084.
2. T. Vijayaraghavan, On the fractional parts of the powers of a number (I), J. London Math. Soc. 15 (1940) 159-160; MR 2,33e.
3. T. Vijayaraghavan, On the fractional parts of the powers of a number (II), Proc. Cambridge Philos. Soc. 37 (1941) 349-357; MR 3,274c.
4. T. Vijayaraghavan, On the fractional parts of the powers of a number (III), J. London Math. Soc. 17 (1942) 137-138; MR 5,35e.
5. L. Flatto, J. C. Lagarias and A. D. Pollington, On the range of fractional parts 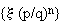, Acta Arith. 70 (1995) 125-147; MR 96a:11073.
6. J. C. Lagarias, The 3x+1 problem and its generalizations, Organic Mathematics, ed. J. Borwein, P. Borwein, L. Jörgenson and R. Corless, Amer. Math. Soc., 1997, pp. 305-334; Amer. Math. Monthly 92 (1985) 3-23; MR 86i:11043.
7. G. H. Hardy and E. M. Wright, An Introduction to the Theory of Numbers, 5th ed. Oxford 1985; MR 81i:10002.
8. C. Small, Waring's problem, Math. Magazine 50 (1977) 12-16; MR 55 #5561.
9. K. S. Brown, Waring's Problem (MathPages).
10. D. Rusin, Waring's Problem (Mathematical Atlas).
11. E. W. Weisstein, Waring's Problem (MathWorld).
12. R. M. Stemmler, The ideal Waring theorem for exponents 401-200,000, Math. Comp. 18 (1964) 144-146; MR 28 #3019.
13. J. M. Kubina and M. C. Wunderlich, Extending Waring's conjecture to 471,600,000, Math. Comp. 55 (1990) 815-820; MR 91b:11101.
14. K. Mahler, On the fractional parts of the powers of a rational number (II), Mathematica 4 (1957) 122-124; MR 20 #33.
15. M. A. Bennett, Fractional parts of powers of rational numbers, Math. Proc. Cambridge Philos. Soc. 114 (1993) 191-201; MR 94h:11062.
16. M. A. Bennett, An ideal Waring problem with restricted summands, Acta Arith. 66 (1994) 125-132; MR 95k:11126.
17. F. Beukers, Fractional parts of powers of rationals, Math. Proc. Cambridge Philos. Soc. 90 (1981) 13-20; MR 83g:10028.
18. A. K. Dubitskas, A lower bound for the quantity 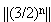, Russian Math. Survey v. 45, n. 4 (1990) 163-164; MR 91k:11058.
19. D. Rusin, A Dense Sequence (Mathematical Atals).
20. A. Miklavc, Elementary proofs of two theorems on the distribution of numbers (mod 1), Proc. Amer. Math. Soc. 39 (1973) 279-280; MR 47 #4962.
21. M. Drmota and R. F. Tichy, Sequences, Discrepancies and Applications, Lecture Notes in Math. 1651, Springer-Verlag, 1997; MR 98j:11057.
22. W. Forman and H. N. Shapiro, An arithmetic property of certain rational powers, Commun. Pure Appl. Math. 20 (1967) 561-573; MR 35 #2852.
23. R. K. Guy, Unsolved Problems in Number Theory, 2nd ed., Springer-Verlag 1994, section E19; MR 96e:11002.
24. R. Balasubramanian, J.-M. Deshouillers and F. Dress, numerous articles, reviewed in MR 87m:11098, MR 87m:11099, MR 88a:11099, MR 88e:11095, MR 94c:11096, MR 94g:11079, MR 94b:11101.
25. M. Waldschmidt, Transcendence Methods, Queen's Papers in Pure and Appl. Math., n. 52, ed. A. J. Coleman and P. Ribenboim, Queen's University, 1979; MR 83a:10068.
26. M. Waldschmidt, On the transcendence method of Gelfond and Schneider in several variables, from New Advances in Transcendence Theory, ed. A. Baker, Cambridge Univ. Press, 1988; MR 90d:11089.
27. A. M. Odlyzko and H. S. Wilf, Functional iteration and the Josephus problem, Glasgow Math. J. 33 (1991) 235-240; MR 92g:05006.
28. L. Habsieger, Minorations de ||(3/2)^k||, (1991-1992 INRIA lecture).
29. R. Blecksmith, M. McCallum and J. L. Selfridge, 3-smooth representations of integers, Amer. Math. Monthly 105 (1998) 529-543; MR 2000a:11019.
30. M. R. Avidon, On primitive 3-smooth partitions of n, Elec. J. Combin. 4 (1997); MR 98a:11136.
31. P. Erdös and Mordechai Lewin, d-complete sequences of integers, Math. Comp. 65 (1996) 837-840; MR 96g:11008.
32. P. Erdös and R. Graham, Old and New Problems and Results in Combinatorial Number Theory, Enseign. Math. Mono. 28 (1980), p. 80; MR 82j:10001.
33. I. Vardi, Computational Recreations in Mathematica, Addison Wesley 1991, pp. 20-25; MR 93e:00002.
34. G. H. Hardy and J. E. Littlewood, Some problems of Diophantine approximation, Acta Math. 37 (1914) 155-191; Collected Papers of G. H. Hardy, v. 1, Oxford Univ. Press, 1966, pp. 28-66.
35. C. Pisot, La répartition modulo 1 et les nombres algébriques, Ann. Scuola Norm. Sup. Pisa 7 (1938) 205-248.
36. L. E. Dickson, Proof of the ideal Waring theorem for exponents 7-180, Amer. J. Math. 58 (1936) 521-529.
37. L. E. Dickson, Solution of Waring's problem, Amer. J. Math. 58 (1936) 530-535.
38. S. S. Pillai, On Waring's problem, J. Indian Math. Soc. 2 (1936) 16-44; Zentralblatt 14/294.
39. H. Weyl, Über die Gleichverteilung von Zahlen mod. Eins, Math. Annalen 77 (1916) 313-352.

Copyright © 1995-2001 by Steven Finch.
All rights reserved.